Dropdown (One Answer) question sample:

The Dropdown (Many Answers) question lets the respondent choose more than one answer from a dropdown list of choices.

For example, in a customer satisfaction survey you're conducting at your cafe, you could ask your customers about their preferences for adding a new variety of cold beverages.

Dropdown (Many Answers) question sample:

To add a dropdown (one answer/many answers) question in your survey:

1. Click Dropdown (One Answer) or Dropdown (Many Answers) in the question types listed on the left pane. You can also drag and drop the question type to the builder. To change the question type, you can click the dropdown next to the question type's name in the question editor. However, the choices for change are related to the question type you have selected. For example, if you selected a dropdown question type, you can only change it to its variants available in the dropdown list.
   
   
   
2. In the Question box, type your question.
   
1. If you want to mark the question mandatory, select the Make this question mandatory checkbox.
   
2. If you want to make changes to the default Error message text that displays, edit the content in the text box.
3. In the Required number of choices dropdown list, select the number of rows you want to keep as mandatory. This can be in the form of at least, at most, exactly, or in between. This option appears only if the Make this question mandatory checkbox is selected.
4. If you want to pipe in custom variables or variables from previous questions and customize the follow-up questions, click Insert Variable right above the Question box, and select the variable you want to use from the list. Read more on Piping.
   
3. In the Choice section, you can add the answer choices in the following ways:
   
1. If you are copying and pasting the choices in the Answer box, make sure you type in each choice on a separate line. 
   
   
   
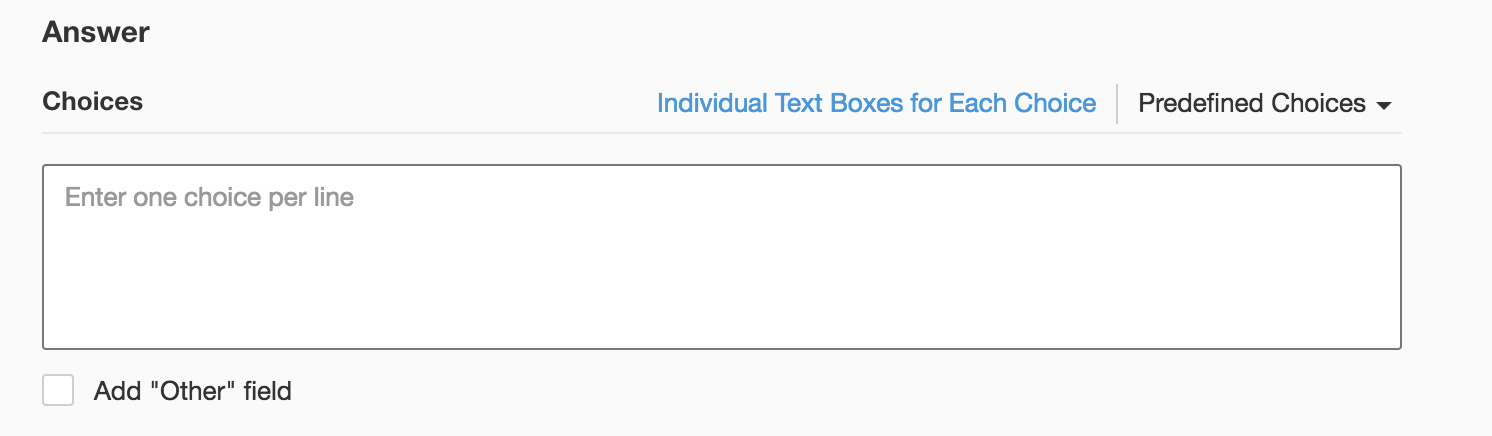
2. If you want to add choices separately, click Individual Text Boxes for Each Choice right above the Answer box, and start adding choices. Click + to add more boxes, and click X to delete choices. 
   
   
   
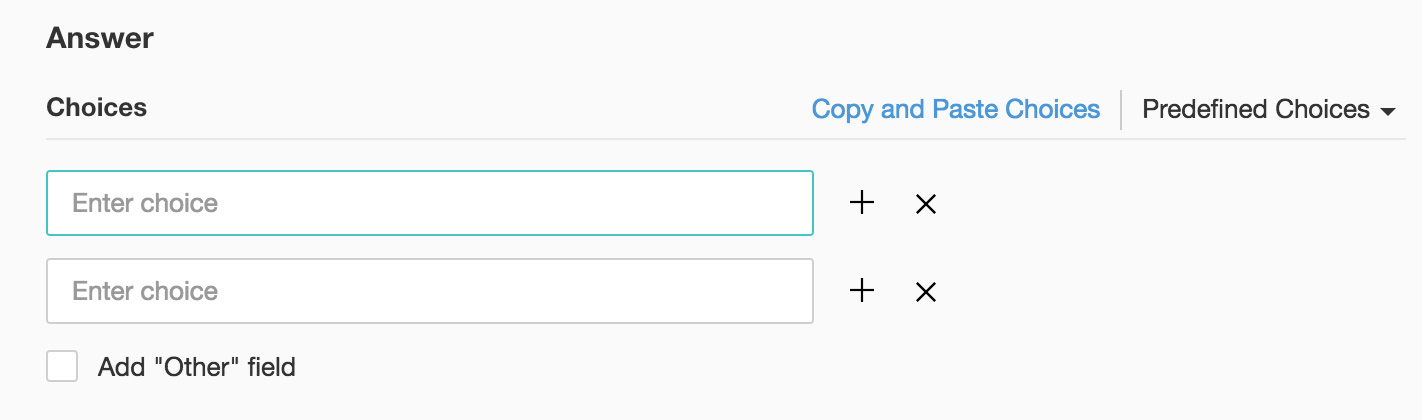
3. If you want to add choices that are predefined, click Predefined Choices and select the choice you want to use in the survey. 
   
   
   
4. If you want to add the Other Choice field along with your answer choices, click Add 'Other' field. If you want to make changes to the default Field label text that displays, edit the content in the text box. 
   
4. To learn what else you can do with the question, click Advanced options. You can perform the following actions: 
   
1. Select Change the order of choices. You can perform the following actions here:
   
1. Randomize for each respondent - To change the order randomly for each respondent
   
2. Flip for each respondent - To show the choices in the opposite order for each respondent
   
3. Rotate for each respondent - To rotate the choices for each respondent
   
4. Ascending sort - To arrange the choices in the ascending order
   
5. Select Don't randomize the last few choices if you want to select the number of choices that needn't be randomized
   
2. To add a comments box, select Add 'Comments'  field. If you want to change the name of the field, in the Comments field label box, type in the new field name.
   
3. The autofill or prepopulate answer feature allows you to prepopulate single-variable survey responses automatically before sending them to the respondents. To prepopulate answers for a known respondent, select Prepopulate answer.
   
   In addition, disable the Editable checkbox to restrict the responders from editing the pre-populated answer you have configured.
4. Question hint is used to add hints to your question and help your respondents get a clear idea of what your questions are all about. This feature is optional and is available only for certain types of questions. 
   
   
   
5. Switch to the Display Logic and Answer Display Logic tabs to add a logic condition to the question and answer choices respectively.
   
6. To save the changes, click Save.
   
7. To discard the changes, click Cancel.